boolean-algebra
Class-11

বুলীয় বীজগণিত | Boolean Algebra

Posted on Author JUMP Magazine Comments Off on বুলীয় বীজগণিত | Boolean Algebra
কম্পিউটার – একাদশ শ্রেণি – বুলীয় বীজগণিত

আমরা কিছু সমস্যার সমাধান করতে করতে এসো শিখে নিই Boolean Algebra।

1. একটি full order এর truth table লেখ এবং k-map ব্যবহার করে তার Boolean expression নির্ণয় কর এবং তার logic diagram অঙ্কন কর।

আমরা জানি যে full order হল এমন একটি combinational logic circuit যা তিনটি bit কে যোগ করতে পারে। ধরা যাক কোন full order এর দুটি input হল x এবং y। আরও ধরা যাক z হল carry bit, যা তৃতীয় input হিসাবে কাজ করবে। Full order এর দুটি output হিসাবে s (sum) এবং c (carry) পাওয়া যায়।

Full order এর truth table হল:

যেহেতু full order এর sum এবং carry দুটি output পাওয়া যায়, তাই দুটি পৃথক Karnaugh map ব্যবহার করে তাদের boolean expression আমাদের নির্ণয় করতে হবে।
Sum (s) এর জন্য Karnaugh map করলে আমরা পাই:

∴ Sum এর boolean expression হল s = \bar{x}y{z} + x\bar{yz} + \bar{xy}z + xyz
= \bar x(y\bar{z} + \bar{y}z) + x(\bar{yz}+ yz)
= \bar{x} (y \oplus z) + x(y \oplus z)
= x \oplus y \oplus z
এটি একটি 3 input XOR gate এর output।
Carry (c ) এর জন্য Karnaugh map করলে আমরা পাই:

∴ Karnaugh map থেকে আমরা carry এর boolean expression পাই:
c = xy + yz + xz

আমরা জানি যে full order এর carry (c) = (x \oplus y)z + xy। Karnaugh map কিন্তু ব্যবহার করে আমরা xy + yz + xz কে carry এর boolean expression হিসাবে পাই।

একাদশ শ্রেনি থেকে → বাংলা | ইংরাজি

এই expression কে (x \oplus y)z + xy আকারে প্রকাশ করা যায়।

c = xy + yz + xz
= xy(z + \bar{z}) + yz(x + \bar{x}) + xz(y + \bar{y}) [∵x + \bar{x} = 1, y + \bar{y} = 1, z + \bar{z} = 1]
= xyz + xy\bar{z} + xyz + \bar{x}yz + xyz + x\bar{y}z
= xyz + xy\bar{z} + x\bar{y}z + \bar{x}yz [∵ xyz + xyz + xyz = xyz]
= xy(z + \bar{z}) + z(x\bar{y} + \bar{x}y)
= xy + z(x \oplus y) [∵x\bar{y} + \bar{x}y = x \oplus y, z + \bar {z} = 1]
∴ Full order এর boolean expression হল:
Sum (s) = x \oplus y \oplus z
Carry (c) = xy + z(x \oplus y)

2. F = π (0, 2, 4, 5) এর truth table ও logical expression লেখ।

∴ Logical expression হল: F = (x + y + z). (x + {y} + z). (\bar{x} + y + z). (\bar{x}+ y +\bar{z})। (উত্তর)

3. F (x, y, z) = y (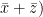\bar{x} + \bar{z}) কে sum of product (SOP) বা minterm এর sum রূপে প্রকাশ কর।

আমরা জানি যে Minterm এ প্রকাশ করার জন্য যেসব output এর value 1, তাদের যোগ করতে হয়।
∴ Sum of product হল: F = \bar{x}y\bar{z} + \bar{x}yz + xy\bar{z} (উত্তর)

4. F (x, y, z) =\sum (0,2,3,4,7) কে maxterm এর গুণ আকারে প্রকাশ কর।

আমরা জানি যে তিনটি চলরাশি বা variable এর জন্য মোট 2^3 = 8 টি পদ হয়। এখানে প্রদত্ত minterm এ 0, 2, 3, 4, 7 আছে। সুতরাং বাকী 1, 5, 6 এই তিনটি maxterm এ উপস্থিত থাকবে।
∴ Maxterm হবে π (1, 5, 6)

∴ Maxterm এর গুণফল product of sum (POS) হল: F = (x + y +\bar{z}). (\bar{x} + y + \bar{z}). (\bar{x} + \bar{y} + z). (Ans)

4. Universal gate বা সার্বজনীন গেট কাকে বলে? প্রমাণ কর NOR একটি Universal gate।

যে সব gate ব্যবহার করে তিনটি fundamental gate অর্থাৎ AND, OR এবং NOT এই তিনটি gate কে তৈরি করা যায়, তাদের সার্বজনীন গেট বা Universal gate বলা হয়।

উদাহরণ- NAND gate, NOR gate.

একাদশ শ্রেণি থেকে → Physics | Chemistry | Biology | Computer

ধরে নেওয়া যাক কোন two input NOR gate এর দুটি input হল A ও B তাহলে ওই NOR gate এর output হবে f =\overline{A+B}।

NOR gate কে Universal gate প্রমাণ করতে হলে আমাদের শুধুমাত্র NOR gate ব্যবহার করে AND, OR, NOT gate তৈরি করতে হবে।

a) NOR gate থেকে AND gate— কোন NOR gate এর A এবং B input কে \bar{A} ও \bar{B} দিয়ে replace করা হলে তা AND gate এর মতন কাজ করে।

এখানে দুটি NOR gate এ A এবং B input পাঠানো হল। হিসাবে যে পাওয়া গেল তাদের তৃতীয় NOR gate এ input করা হলে আমরা যে final output পাই তা হল:

f =\overline{\overline{A}+\overline{B}}
= \overline{\overline{A}}.\overline{\overline{B}}
= A.B যা একটি two input AND gate এর output

b) NOR gate থেকে OR gate— A ও B input যুক্ত কোন NOR gate এর output কে অন্য একটি 2 input NOR gate এর input হিসাবে পাঠানো হলে তা OR gate এর মতন কাজ করে।

এখানে A ও B input যুক্ত প্রথম NOR gate থেকে প্রাপ্ত \overline{A+B} এই output কে দ্বিতীয় NOR gate এর input হিসাবে পাঠানো হল। এখানে প্রাপ্ত final output হল:

f =\overline{\overline{A+B}+\overline{A+B}}
=\overline{\overline{A+B}}.\overline{\overline{A+B}}
= \overline{\overline{A+B}}
= A + B, যা একটি 2 input OR gate এর output

c) NOR gate থেকে NOT gate— NOR gate এর দুটি input যদি একই হয় তাহলে তার output সবসময় input এর পরিপূরক বা complement হয়।
ফলে এটি NOT gate এর কাজ করে।

এখানে NOR gate এর B input কে A দ্বারা replace করা হয়েছে, অর্থাৎ এখানে দুটি input একই এবং তা হল A। এর ফলে আমরা যে output পাই তা হল:

f = \overline{A+A}
=\overline{A}.\overline{A}
= A, যা একটি NOT gate এর output

যেহেতু NOR gate ব্যবহার করে AND, OR, NOT gate এই তিনটি মূল বা fundamental gate তৈরি করা সম্ভব হল, সুতরাং NOR gate একটি Universal gate বা সার্বজনীন গেট।

5. সরল (Simplify) কর:

\bar{A}(A + B) + (B + AA) (A + \bar{B})
\bar{A}(A + B) + (B + AA) (A + \bar{B})
= \bar{A}. A + \bar{A}. B + (B + A) (A + \bar{B}) [∵ A. A = A]
= 0 + \bar{A}. B + BA + AA + B\bar{B} + A\bar{B} [∵ {A}. A = 0]
= \bar{A}B + AB + A + 0 + A\bar{B} [∵ A. A = A, {B}. B = 0]
= B(\bar{A} + A) + A(1 + \bar{B})
= B.1 + A.1 [∵ {A} + A = 1, 1 + \bar{B} = 1]
= A + B (উত্তর)

6. দুটি Half adder ব্যবহার করে Full adder তৈরি কর এবং sum ও carry নির্ণয় কর।

ধরি তিনটি input হল x, y, z. এই তিনটি input ব্যবহার করে দুটি Half adder ব্যবহার করে Full adder তৈরি করা যায়।

একটি two input half adder ক্ষেত্রে sum (s^1) = \bar{x}y + x\bar{y} এবং carry (c^1) = xy যেখানে x এবং y দুটি input।

এবার দুটি half adder দিয়ে একটি full adder তৈরি করতে হলে তাদের input হবে (\bar{x}y + x\bar{y}) এবং z।

এবার sum ও carry হিসাব করলে পাই
Sum (s) = \overline{\overline{x}y+x\bar{y}}.z + (\bar{x}y+x\bar{y}).\bar{z}
=\overline{\overline{x}y.x\overline{y}}.z +\bar{x}y\bar{z} + x\bar{yz}
=(\overline{\overline{x}}+\bar{y})(\bar{x}+\overline{\overline{y}}). z + \bar{x}y\bar{z} + x\bar{yz}
= (x + \bar{y}) (\bar{x} + y). z + \bar{y}\bar{z} + x\bar{yz}
= (x\bar{x} + \bar{xy} + xy + \bar{y}y) z + \bar{x}y\bar{z} + x\bar{yz}
= (0 + \bar{xy} + xy + 0) z + \bar{x}y\bar{z} + x\bar{yz}
= \bar{xy}z + xyz + \bar{x}y\bar{z} + x\bar{yz}
= \bar{x} (\bar{y}z + y\bar{z}) + x (yz + \bar{yz})
= \bar{x} (y \oplus z) + x (\overline{y\oplus z})
= x \oplus y \oplus z

একাদশ শ্রেনি থেকে → বাংলা | ইংরাজি

এটি একটি 3 input Full adder এর sum এর Boolean expression।

Carry (c) = (\bar{x}y + x\bar{y}).\bar{z} + xy
= \bar{x}yz + x\bar{y}z + xy (z + \bar{z})
= \bar{x}yz + x\bar{y}z + xyz + xy\bar{z}
= z (\bar{x}y + x\bar{y}) + xy (z + \bar{z})
= z (x \oplus y) + xy

7. Karanaugh map ব্যবহার করে সমাধান কর: F (A, B, C) = \bar{A}B\bar{C} + AB\bar{C} + ABC

∴ F (A, B, C) = AB + BC^1
= B (A + C^1) (উত্তর)

সমাপ্ত।

এই লেখাটির সর্বস্বত্ব সংরক্ষিত। বিনা অনুমতিতে এই লেখা, অডিও, ভিডিও বা অন্য ভাবে কোন মাধ্যমে প্রকাশ করলে তার বিরুদ্ধে আইনানুগ ব্যবস্থা নেওয়া হবে।

লেখিকা পরিচিতিঃ

বিজ্ঞান স্নাতক এবং কম্পিউটার বিজ্ঞানে উচ্চ শিক্ষিতা নন্দিতা বসুর পেশা শিক্ষকতা।তিনি বই পড়তে বড় ভালোবাসেন। কাজের ফাঁকে, অবসরে, বাসে ট্রামে তো বটেই, শোনা যায় তিনি নাকি ঘুমিয়ে ঘুমিয়েও বই পড়তে পারেন।

এই লেখাটি থেকে উপকৃত হলে সবার সাথে শেয়ার করতে ভুলো না।

JumpMagazine.in এর নিয়মিত আপডেট পাবার জন্য –
JUMP Magazine
https://jumpmagazine.in

Related Articles

kyalorimiti
Class-11

ক্যালোরিমিতি

Posted on Author JUMP Magazine

পদার্থবিদ্যা – একাদশ শ্রেণি – ক্যালোরিমিতি (অধ্যায়- পদার্থের ধর্মসমূহ) তাপবিজ্ঞানের যে শাখায় এক বস্তু থেকে অন্য বস্তুতে সঞ্চালিত তাপের পরিমাণ নিয়ে আলোচনা করা হয় তাকে ক্যালোরিমিতি বলা হয়। সহজভাবে বললে বলা যায় যে, একটি নির্দিষ্ট পরিমাণ উষ্ণতা বৃদ্ধি করার জন্য কোনো বস্তুকে কতটা তাপ দিতে হবে বা উষ্ণতা হ্রাস করার জন্য বস্তু থেকে কতটা তাপ […]
Class-11

উৎসেচকের কার্যপদ্ধতি

Posted on Author JUMP Magazine

Biology – একাদশ শ্রেনি – সজীব কোশের রাসায়নিক গঠন উৎসেচকের কার্যপদ্ধতি বোঝার আগে আমরা একটি বাস্তব উদাহরণ বুঝে নিই। ধরো, তোমার বাড়ি থেকে পায়ে হেঁটে স্কুলে যেতে ২০ মিনিট সময় লাগে। কিন্তু সেখানে তুমি যদি সাইকেল চালিয়ে স্কুলে যাও তাহলে তোমার সময় ও শ্রম দুটোরই অপচয় কম হবে। এক্ষেত্রে সাইকেল না চালিয়ে গেলেও তুমি স্কুলে […]

computer-er-srenibivag
Class-11

কম্পিউটারের শ্রেণিবিভাগ

Posted on Author JUMP Magazine

কম্পিউটার – একাদশ শ্রেনি – কম্পিউটার সিস্টেম (দ্বিতীয় পর্ব) প্রথম কম্পিউটার আবিষ্কার থেকে শুরু করে নানা বিবর্তনের মধ্যে দিয়ে কম্পিউটার আজকের অবস্থায় এসে দাঁড়িয়েছে। সূচনা থেকে আজকের দিন পর্যন্ত বিভিন্ন কাজের প্রয়োজনে তৈরি হয়েছে বিভিন্ন রকম কম্পিউটার। আগের পর্বে আমরা বিভিন্ন প্রজন্মের কম্পিউটার নিয়ে আলোচনা করেছি। এই পর্বে আমরা কম্পিউটারের শ্রেণিবিভাগ নিয়ে আলোচনা করবো। ব্যবহারিক […]