compund interest in bengali
Madhyamik

চক্রবৃদ্ধি সুদ (Compound Interest) | গণিত প্রকাশ

Posted on Author Aditi Sarkar Comments Off on চক্রবৃদ্ধি সুদ (Compound Interest) | গণিত প্রকাশ
শ্রেণি – দশম | বিষয়: গণিত । অধ্যায়: চক্রবৃদ্ধি সুদ

আগের পর্বে আমরা আলোচনা করেছি সরল সুদ নিয়ে। আমারা দেখেছি যে সরল সুদ ব্যবহৃত হয় যখন 1 বছর বা 1 বছরের চেয়েও কম সময়ের জন্য ব্যাংক থেকে টাকা ধার নেওয়া হয়। কিন্তু তার বেশি সময়য়ের জন্য টাকা ধার নেওয়ার ক্ষেত্রে ব্যাংক কিভাবে সুদ হিসাব করবে?

এক বছরের বেশি সময়ের জন্য টাকা ধার নেওয়ার ক্ষেত্রে চক্রবৃদ্ধি সুদ কার্যকরী হয়।

মনে রাখতে হবে, চক্রবৃদ্ধি সুদ শুধুমাত্র আসলের ওপর গণনা করা হয় না, আসল থেকে প্রাপ্ত সুদের ওপরও গণনা করা হয়।

নিম্নে অঙ্কিত ডায়াগ্রামটিতে বিষয়টি স্পষ্ট হবে।

how-compund-interest-worksJPG

আশা করছি, উপরের ডায়াগ্রামটি তোমাদের একটি স্পষ্ট ধারণা দেবে যে কিভাবে চক্রবৃদ্ধি সুদ ব্যবহার করা হয়। এই প্রসঙ্গে একটা কথা বলা প্রয়োজন, চক্রবৃদ্ধি সুদের ধারণার ভিত্তি হল সরল সুদ, তাই তোমাদের যদি সরল সুদের ধারণা পরিষ্কার না থাকে সেক্ষেত্রে সরল সুদের উপর আগের আলোচনা পড়ে নিতে পারো।

jump magazine smart note book

এবার একটি উদাহরণ সহযোগে বুঝব কীভাবে চক্রবৃদ্ধি গণনা করা হয়।

প্রশ্ন এক, 100 টাকার 5% হারে 3 বছরের চক্রবৃদ্ধি সুদ কত?

লক্ষণীয়, প্রথম বছরে শুধু আসলের ওপর সুদ পাওয়া যাবে।

∴ 100 টাকার 5% হারে 1 বছরের সুদ = \frac{100 \times 5 \times 1}{100} = 5 টাকা

∴ প্রথম বছরের সুদ-আসল = 100+5 টাকা = 105 টাকা

এখন প্রথম বছরের সুদ-আসল হল, দ্বিতীয় বছরের আসল।

দ্বিতীয় বছরে 105 টাকার 5% হারে 1 বছরের সুদ = \frac{105 \times 5 \times 1}{100} = 5.25 টাকা

∴ দ্বিতীয় বছরের শেষে সুদ-আসল = 105 + 5.25 = 110.25 টাকা

এবার, তৃতীয় বছরের আসল = 110.25 টাকা

তৃতীয় বছরের সুদ = \frac{110.25 \times 5 \times 1}{100} = 5.5125 টাকা

চক্রবৃদ্ধি সুদ বের করার পদ্ধতি বোঝা গেল। মনে রাখতে হবে, চক্রবৃদ্ধি সুদ ব্যাংকে ধার নেওয়া বা টাকা জমা রাখা উভয়ক্ষেত্রেই প্রযোজ্য।

তাহলে, উপরের অঙ্কে তৃতীয় বছরের শেষে সুদ-আসল কত হল?

110.25 + 5.5125 = 115.7625 টাকা হল তিন বছরের শেষে সুদাসল।

এতো গেল চক্রবৃদ্ধি থেকে পাওয়া সুদ। এখানে যদি সরল সুদে হিসাব করতে হতো, তাহলে কত সুদ পাওয়া যেত?

100 টাকার 5% হারে 3 বছরের সরল সুদ = \frac{100 \times 5 \times 3}{100} = 15 টাকা

∴ 3 বছরের সুদ = 15 টাকা (সরল সুদ)

আর আমরা আগে দেখেছি, 3 বছরের চক্রবৃদ্ধি সুদ = 15.7625 টাকা

সুতরাং প্রতিক্ষেত্রেই চক্রবৃদ্ধি সুদ > সরল সুদ ।

কিন্তু এই প্রক্রিয়ায় চক্রবৃদ্ধি সুদ বেশি বছরের জন্য বের করা বেশ সময়সাপেক্ষ। তাই আমরা সূত্রের সাহায্যে চক্রবৃদ্ধি সুদ নির্ণয় করব।

দশম শ্রেণির অন্য বিভাগগুলি – বাংলা | English | ইতিহাস | ভূগোল

আমাদের অনেকেরই সূত্রটি জানা, যদি আসল = P টাকা, বার্ষিক চক্রবৃদ্ধি সুদের হার = r% হয়, তবে n বছরের শেষে সুদ-আসল = \left ( 1 + \frac{r}{100} \right ) ^{n} টাকা

এবং সুদ = {\left ( 1 + \frac{r}{100} \right ) ^{n} - P} টাকা

কিন্তু সূত্রটি আসছে কীভাবে? একবার বুঝে নেওয়া যাক।

আসল = P, বার্ষিক চক্রবৃদ্ধি সুদ  r হলে,

1 বছরের শেষে সুদ = \frac{P \times 1 \times r}{100} = \frac{Pr}{100}

∴ 1 বছরের শেষে সুদ-আসল তথা, দ্বিতীয় বছরের আসল = P + \frac{Pr}{100} = P (1 + \frac{Pr}{100}) টাকা

∴ দ্বিতীয় বছরের শেষে সুদ → \frac{P\left ( 1 + \frac{r}{100} \right )\times 1\times r}{100}

∴ দ্বিতীয় বছরের শেষে সুদ-আসল = P (1 + \frac{r}{100}) + \frac{P\left ( 1 + \frac{r}{100} \right )\times r}{100}

= P (1 + \frac{r}{100}) × 1 + \frac{r}{100}

= P \left ( 1 + \frac{r}{100} \right ) ^{2}

এইভাবে ক্রমশ n তম বছরের শেষে সুদ-আসল → P \left ( 1 + \frac{r}{100} \right ) ^{n} টাকা।

এবার, পূর্বের অংকটি এই পদ্ধতিতে করে উত্তরটি যাচাই করে নেওয়া যাক।

100 টাকার 5% হারে 3 বছরের চক্রবৃদ্ধি সুদ-আসল → 100 \left ( 1 + \frac{5}{100} \right ) ^{3}

= 100 \left ( 1 + \frac{1}{20} \right ) ^{3}

= 100\times \frac{21}{20}\times \frac{21}{20}\times \frac{21}{20}

= 115.7625

∴ চক্রবৃদ্ধি সুদ = 115.7625 – 100 = 15.7625 টাকা

দশম শ্রেণির অন্য বিভাগগুলি – গণিত | জীবনবিজ্ঞান | ভৌতবিজ্ঞান

অনেক ক্ষেত্রেই 6 মাস অন্তর বা 3 মাস অন্তর চক্রবৃদ্ধি সুদ নির্ণয়ের প্রয়োজন পড়ে। সেক্ষেত্রে কীভাবে করব?

সূত্রের সাহায্যে শেখার পূর্বে মূল নিয়মের সাথে বুঝে নেওয়া যাক।

পূর্বের অঙ্কেই যদি প্রশ্নে থাকত, 6 মাস অন্তর দেয় বার্ষিক 5% চক্রবৃদ্ধি হার সুদে 100 টাকার 1 বছরের চক্রবৃদ্ধি সুদ কত? তবে কীভাবে তা করতে হবে সেটা বুঝে নেওয়া যাক।

আমরা পূর্বেই জেনেছি 6 মাস = ½ বছর

100 টাকার 5% হারে 6 মাসের সুদ = \frac{100\times \frac{1}{2}\times 5}{100}

= \frac{5}{2} = 2.5 টাকা।

jump magazine smart note book

আমাদের 1 বছরের 8টি চক্রবৃদ্ধি সুদ নির্ণয় করতে হবে।

সুতরাং প্রথম 6 মাসের আসল 100 টাকা  হলেও, পরের 6 মাসের আসল 100 টাকা হবে না।

পরের 6 মাসের আসল = প্রথম 6 মাসের আসল + প্রথম 6 মাসের সুদ

= 100 + 2.5

= 102.5 টাকা

∴ পরের 6 মাসের সুদ = \frac{102.5\times \frac{1}{2}\times 5}{100} = 2.5625 টাকা।

1 বছরের 5% চক্রবৃদ্ধি হারে সুদ আসল = 102.5 + 2.5625 = 105.0625 টাকা

∴ সুদ = 5.0625 টাকা

এই অঙ্কটি সূত্রের সাহায্যে কীভাবে করব বুঝে নেওয়া যাক।

আমরা জানি, P টাকার r% হারে n বছরের চক্রবৃদ্ধি সুদ-আসল → P \left ( 1 + \frac{r}{100} \right ) ^{n} টাকা।

এখন n = 1 বছর । কিন্তু সুদ 6 মাস অন্তর হওয়ায়, 1 বছরে দুবার সুদ নির্ণয় করতে হবে।

∴ N = 2 হবে।

তবে r = 5% হল বার্ষিক সুদ

সুতরাং 6 মাসের সুদ = \frac{r}{2} = \frac{5}{2} = 2.5%

∴ নির্ণেয় সুদাসল = 100 \left ( 1 + \frac{2.5}{100} \right ) ^{2} টাকা।

= 100\times \frac{102.5}{100}\times \frac{102.5}{100} = 105.0625

= 105.0625

∴ চক্রবৃদ্ধি সুদ = 5.0625 টাকা

অর্থাৎ এই type এর অঙ্কে দেখে নেওয়া প্রয়োজন বছরকে কতগুলি মাস হিসাবে কত বার ভাঙছে।

এক্ষেত্রে, 6 মাস অন্তর হলে, সূত্র হবে 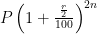P \left ( 1 +\frac{\frac{r}{2}}{100} \right )^{2n}

jump magazine smart note book

নিজে করো:  3 মাস অন্তর দেয় বার্ষিক 8% চক্রবৃদ্ধি হার সুদে 10000 টাকার 9 মাসের চক্রবৃদ্ধি সুদ হিসেব কর।

প্রশ্ন দুই, বার্ষিক চক্রবৃদ্ধি সুদের হার প্রথম বছর 4% এবং দ্বিতীয় বছর 5% হলে, 25,000 টাকায় 2 বছরের চক্রবৃদ্ধি সুদ কত?

স্পষ্টতই প্রথম বছরের সুদাসল হবে দ্বিতীয় বছরের আসল, কারণ চক্রবৃদ্ধি সুদ নির্ণয় করতে হবে।

মূল পদ্ধতিতে নির্ণয় পাঠকদের জন্য তোলা থাকল।

আমরা প্রশ্নটি সূত্রের সাহায্যে সমাধান করার আগে, সূত্রটি একবার জেনে নিই।

চক্রবৃদ্ধি সূত্র নির্ণয়ের  সময়, আমরা প্রথম বছরের সুদাসল পেয়েছিলাম  P \left ( 1 + \frac{r}{100} \right ) ^{n} যা দ্বিতীয় বছরের আসল ।

এখন প্রথম বছরের সুদ r1 %,

দ্বিতীয় বছরের সুদ r2 % হলে,

প্রথম বছরের সুদাসল হল = P\left ( 1+ \frac{r_{1}}{100} \right )

দ্বিতীয় সুদাসল = \frac{P\left (1 + \frac{r_{1}}{100} \right )\times 1\times r_{2}}{100} + P\left ( 1+ \frac{r_{1}}{100} \right )

= P\left ( 1+ \frac{r_{1}}{100} \right ) \left \{ \frac{r_{2}}{100} + 1 \right \}

= P\left ( 1+ \frac{r_{1}}{100} \right ) \left ( 1+ \frac{r_{2}}{100} \right)

এই প্রশ্নে,

r1 = 4, r2 = 5, P = 25,000

∴ সুদাসল = 25,000 \left ( 1 + \frac{4}{100} \right )\times \left ( 1 + \frac{5}{100} \right ) টাকা

= 27,300 টাকা

∴ সুদ = 27,300 – 25,000 = 2300 টাকা।

আরো পড়ো  – সমহার বৃদ্ধি ও হ্রাস


Join JUMP Magazine Telegram

JumpMagazine.in এর নিয়মিত আপডেট পাওয়ার জন্য –

X-Math-6a

Aditi Sarkar
রাজাবাজার সায়েন্স কলেজের ফলিত গণিতের (MSc in Applied Mathematics) প্রাক্তন ছাত্রী অদিতি সরকারের গণিতের সাথে সম্পর্ক চিরকালীন। পড়াশোনার পাশাপাশি গান শুনতে ও ছবি আঁকতে ভালোবাসেন অদিতি।

Related Articles

shikkha-sonogskar-boishistho-porjalocona
Madhyamik

উনিশ শতকের বাংলা- শিক্ষা সংস্কার: বৈশিষ্ট্য ও পর্যালোচনা

Posted on Author JUMP Magazine

ইতিহাস – দশম শ্রেণি – শিক্ষা সংস্কার: বৈশিষ্ট্য ও পর্যালোচনা (পর্ব – ২) আগের পর্বে আমরা সাময়িকপত্র, সংবাদপত্র ও সাহিত্য সম্পর্কে জেনেছি এই পর্বে আমরা উনিশ শতকের বাংলা- শিক্ষা সংস্কার: বৈশিষ্ট্য ও পর্যালোচনা সম্পর্কে আলোচনা করবো। প্রাচ্য শিক্ষা -পাশ্চাত্য শিক্ষা বিষয়ক দ্বন্দ ভারতবর্ষে কোম্পানির শাসন প্রতিষ্ঠিত হওয়ার পর ভারতীয়দের শিক্ষার প্রসারের জন্য ইংরেজ শাসকরা প্রথম […]

bharater-vuprokriti
Madhyamik

ভারতের ভূপ্রকৃতি | আঞ্চলিক ভূগোল

Posted on Author JUMP Magazine

ভূগোল – দশম শ্রেণি – আঞ্চলিক ভূগোল (দ্বিতীয় পর্ব) আগের পর্বে আমরা ভারতের অবস্থান ও তার প্রশাসনিক বিভাগ নিয়ে আলোচনা করেছি। এই পর্বে আমরা ভারতের ভূপ্রকৃতি সম্পর্কে আলোচনা করবো। ভূপ্রকৃতি কাকে বলে? আমরা আমাদের চারপাশে তাকালেই প্রকৃতির বিভিন্ন রূপ বৈচিত্র্য দেখতে পাই। কোথাও বা উঁচু পর্বতমালা, কোথায় মাইলের পর মাইল বালি দিয়ে ঘেরা মরুভূমি, কোথায় […]
Madhyamik

নব নব সৃষ্টি – দ্বিতীয় পর্ব

Posted on Author JUMP Magazine

বাংলা – নবম শ্রেনি – নব নব সৃষ্টি (দ্বিতীয়পর্ব) নব নব সৃষ্টি প্রবন্ধের প্রথম পর্বের আলোচনায় আমরা লেখক পরিচিতি, উৎস এবং বিষয়সংক্ষেপ (প্রথম অংশ) নিয়ে আলোচনা করেছি। আগের পর্বটি পড়া না থাকলে এই লিঙ্ক থেকে পড়ে নেবার অনুরোধ রইল – নব নব সৃষ্টি (প্রথম পর্ব)। বিষয়সংক্ষেপ (দ্বিতীয় অংশ) বাংলা ভাষার উৎস সংক্রান্ত আলোচনার পরে প্রাবন্ধিক […]