বিষয়: গণিত ।নবম শ্রেণি । অধ্যায়: সূচক (পর্ব দুই)
আগের পর্বে আমরা সূচকের ধারণা সম্পর্কে আলোচনা করেছি, এই পর্বে আমরা সূচকের নিয়মাবলী সম্পর্কে বিস্তারিত আলোচনা করবো। আগের পর্ব পড়া না থাকলে আগের পর্বটি এই লিঙ্ক থেকে পড়ুন।
সূচকের নিয়মাবলী
যদি m ও n অখন্ড সংখ্যা হলে, এবং ও
হলে;
নিয়ম ১। 
উদাহরণঃ
আমরা জানি এর মান হল
এবার একই সমস্যায় সূচকের নিয়ম প্রয়োগ করে পাই –
তোমারা আরো ভালো ভাবে ব্যাপারটা বোঝার জন্য, নিজেরাও বিভিন্ন সংখ্যা দ্বারা যাচাই করতে পারো।
নিয়ম ২। 
উদাহরণঃ
সূচকের নিয়ম ব্যবহার করে পাই।
আবার,
অর্থাৎ, সূচক বা সাধারণ নিয়ম দুটি ক্ষেত্রেই ফলাফল একই।
একটা ব্যাপার বিশেষ ভাবে লক্ষ্যনীয়,

নিয়ম ৩। 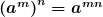
উদাহরণঃ
=
=
=
নিয়ম ৪। 
উদাহরণঃ
=
=
আবার,
=
=
নিয়ম ৫। 
এর উদাহরণ প্রমাণের দায়িত্ব তোমাদের জন্য রইল।
নবম শ্রেণির অন্য বিভাগগুলি – গণিত | জীবনবিজ্ঞান | ভৌতবিজ্ঞান
নিয়ম ৬। 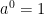
প্রমান,
নিয়ম ৭। 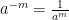
⇒
= [
]
নবম শ্রেণির অন্য বিভাগগুলি – বাংলা | English | ইতিহাস | ভূগোল
এই লেখাটির সর্বস্বত্ব সংরক্ষিত। বিনা অনুমতিতে এই লেখা, অডিও, ভিডিও বা অন্যভাবে কোনো মাধ্যমে প্রকাশ করলে তার বিরুদ্ধে আইনানুগ ব্যবস্থা নেওয়া হবে।
এই লেখাটি থেকে উপকৃত হলে সবার সাথে শেয়ার করার অনুরোধ রইল।
JumpMagazine.in এর নিয়মিত আপডেট পাওয়ার জন্য –
- ফলো করো – WhatsApp চ্যানেল
- সাবস্ক্রাইব করো – YouTube চ্যানেল
- লাইক করো – facebook পেজ
- সাবস্ক্রাইব করো – টেলিগ্রাম চ্যানেল
- Facebook Group – লেখা – পড়া – শোনা
IX_M_2b






